As I just got started on my classes for my master's degree, I thought I'd start posting about the most interesting thing I'm learning so far. That would be orbital mechanics. So here are some basic basics (borrowing heavily from the textbook To Rise from Earth by Wayne Lee).
Types of orbits and characteristics
Orbits come in different shapes and sizes. In the early 1600s, Kepler first described orbits as elliptical and, in fact, they all are. We typically think of them as circular, but this is only a special case. In reality, every orbit is slightly elliptical. The point at which the satellite is closest to the Earth is call the perigee and the point at which it is farthest is called the apogee.
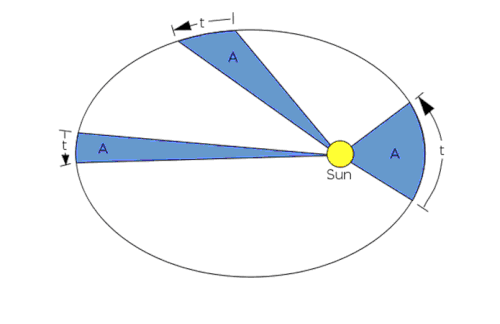
Kepler also observed that the area per time swept out by the arc of the satellite's orbit is equal across the entire orbit. Translated into the English: the satellite moves faster during the parts of its orbit when it is closer to Earth, and moves more slowly the further it is away.
An orbit that moves from west to east (counter clockwise when looking down from the north pole) is said to be a "posigrade orbit" and one moving from east to west is said to be a "retrograde orbit."
Orbital changes
If you ignore effects like atmospheric drag and such, satellites will generally settle into a stable (elliptical) orbit of some kind. So in order to give it a new orbit, you have to change its momentum. This generally utilizes thrusters of some kind. By firing thrusters and changing the direction of motion, you can bump the satellite from one orbit to another. Of note, the initial orbit and the final orbit will always overlap at the burn point.
If you start with a roughly circular posigrade orbit and you initiate a posigrade burn, you'll increase the satellite's velocity and fling it farther out into space. The resulting orbit will be elliptical, with the perigee at the burn point. And because orbits further out are slower, the resulting elliptical orbit will also be slower (which is counter intuitive since you increased its velocity with the burn.
Conversely, if you initiate a retrograde burn, you slow the satellite down and allow it to fall closer to the Earth, which actually makes it orbit faster. You can also do the opposite to make an elliptical orbit more circular. Namely if you start with an elliptical orbit and initiate a posigrade burn at apogee (i.e. speed it up when it is at its slowest), you can move the satellite onto a circular orbit with the altitude equal to the apogee of the previous orbit. Or you can initiate a retrograde burn at perigee (i.e. slow it down when it is at its fastest) and move the satellite onto a circular orbit with an altitude equal to the perigee of the previous orbit.
The Hohmann Transfer
Typically, you're not trying to get a satellite from a circular orbit onto an elliptical one. You're trying to get it from one circular orbit to another, but you cannot do this directly. The simplest (but not the fastest) way to do this is by utilizing an intermediary elliptical orbit. To go from a lower altitude circular orbit to a higher one, initiate a posigrade burn such that the apogee of the new elliptical orbit will be at the altitude of the desired circular orbit. Once the satellite gets to apogee, initiate another posigrade burn to circularize the orbit.
To go from a higher altitude circular orbit to a lower one, do two retrograde burns (only this time the first burn will then mark the apogee of the new elliptical orbit, causing the satellite to fall inward toward the new perigee. Then at perigee give the second retrograde burn to circularize the orbit).
Rendezvous maneuvers
I figured I'd end with rendezvous maneuvers. Now you know how to get from one circular orbit to another. So let's say you're on a mission to rendezvous with a satellite to fix it. You've made it to the same orbit as the satellite, but it's 10 minutes ahead of you on the orbit. How do you catch up? Two key points to remember: 1) a new orbit will always touch the old orbit at the burn point and 2) a smaller orbit revolves around the Earth more quickly.
So in the hypothetical case above, if the orbit I'm on (and that the satellite is on) takes two hours to revolve around the Earth, I could initiate a retrograde burn to slow me down and let me fall towards the Earth in a smaller elliptical orbit. This new orbit will revolve around the Earth faster and I'll get back to apogee (the burn point) sooner. If I calculate it out right, I would want this new orbit to take only 1 hour 50 minutes, so that I arrive at the burn point exactly 10 minutes ahead of when I would have otherwise. At that point, I can fire a posigrade burn and re-circularize my orbit just in time to meet up with the satellite.
Paradoxically, you have to slow down in order to catch up. Words that could be applied to so many aspects of life...